EM 算法-对鸢尾花数据进行聚类

公号：码农充电站pro

主页：https://codeshellme.github.io

之前介绍过K 均值算法，它是一种聚类算法。今天介绍EM 算法，它也是聚类算法，但比K 均值算法更加灵活强大。

EM 的全称为 Expectation Maximization，中文为期望最大化算法，它是一个不断观察和调整的过程。

1，和面过程

我们先来看一下和面的过程。

通常情况下，如果你事先不知道面与水的比例，和面过程可能是下面这样：

1. 先放入一些面和水。
2. 将面团揉拌均匀。
3. 观察面团的稀稠程度：如果面团比较稀，则加入少许面；如果面团比较稠，则加入少许水。
4. 如此往复第2，3步骤，直到面团的稀稠程度达到预期。

这个和面过程，就是一个EM 过程：

• 先加入一些面和水，将面团揉拌均匀，并观察面团的稀稠程度。这是E 过程。
• 不断的加入水和面（调整水和面的比例），直到达到预期面团程度。这是M 过程。

2，再看K 均值算法

在介绍K 均值 聚类算法时，展示过一个给二维坐标点进行聚类的例子。

我们再来看一下这个例子，如下图：

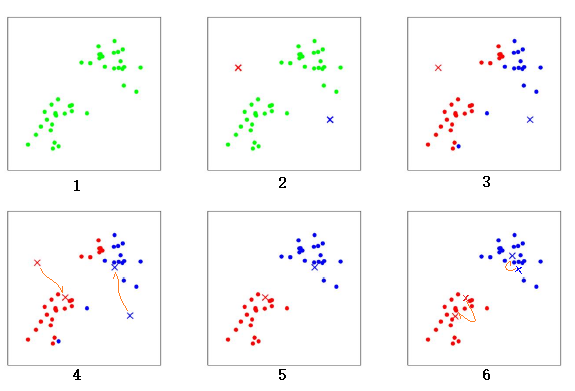
上图是一个聚类的过程，共有6 个步骤：

1. 初始时散点（绿色点）的分布。
2. 随机选出两个中心点的位置，红色x 和蓝色x。
3. 计算所有散点分别到红色x 和蓝色x的距离，距离红色x 近的点标红色，距离蓝色x近的点标蓝色。
4. 重新计算两个中心点的位置，两个中心点分别移动到新的位置。
5. 重新计算所有散点分别到红色x 和蓝色x的距离，距离红色x 近的点标红色，距离蓝色x近的点标蓝色。
6. 再次计算两个中心点的位置，两个中心点分别移动到新的位置。中心点的位置几乎不再变化，聚类结束。

经过以上步骤就完成了一个聚类过程。

实际上，K 均值算法也是一个EM 过程：

• 确定当前各类中心点的位置，并计算各个散点到现有的中心点的距离。这是E 过程。
• 将各个散点归属到各个类中，重新计算各个类的中心点，直到各类的中心点不再改变。这是M 过程。

3，EM 算法

将二维数据点的聚类过程，扩展为一般性的聚类问题，EM 算法是这样一个模型：对于待分类的数据点，EM 算法让计算机通过一个不断迭代的过程，来构建一个分类模型。

EM 算法分为两个过程：

• E 过程：根据现有的模型，计算各个数据输入到模型中的计算结果，这称为期望值计算过程，即 E 过程。
• M 过程：重新计算模型参数，以最大化期望值，这称为最大化过程，即M 过程。

以二维数据点的聚类过程为例，我们定义：

• 同一类中各个点到该类中心的平均距离为 d；
• 不同类之间的平均距离为 D。

那么二维数据点聚类的M 过程，就是寻求最大化的D 和 -d。我们希望的聚类结果是，同一类的点距离较近，不同类之间距离较远。

EM 算法不是单个算法，而是一类算法。只要满足EM 这两个过程的算法都可以被称为EM 算法。常见的EM 算法有GMM 高斯混合模型和HMM 隐马尔科夫模型。

4，最大似然估计

高等数学中有一门课叫做《概率论与数理统计》，其中讲到了参数估计。

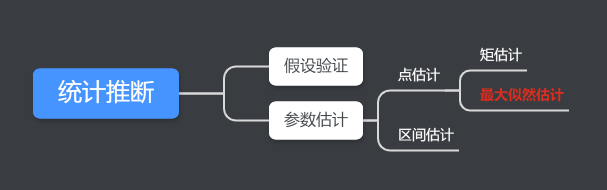
统计推断是数理统计的重要组成部分，它是指利用来自总体的样本提供的信息，对总体的某些特征进行估计或推断，从而认识整体。

统计推断分为两大类：参数估计和假设检验。

我们假设，对于某个数据集，其分布函数的基本形式已知，但其中含有一个或多个未知参数。

参数估计就是讨论如何根据来自总体的样本提供的信息对未知参数做出估计。参数估计包括点估计和区间估计。其中，点估计中有两种方法：矩估计法和最大似然估计法。

最大似然估计是一种通过已知结果，估计未知参数的方法。

5，EM 算法原理

EM 算法使用的是最大似然估计的原理，它通过观察样本，来找出样本的模型参数。

下面通过一个投硬币的例子，来看下EM 算法的计算过程。

这个例子来自《Nature》（自然）期刊的论文《What is the expectation maximization algorithm？》（什么是期望最大化算法？）。

假定有两枚不同的硬币 A 和 B，它们的重量分布 θ_A​ 和 θ_B​ 是未知的，则可以通过抛掷硬币，计算正反面各自出现的次数来估计θ_A​ 和 θ_B​。

方法是在每一轮中随机抽出一枚硬币抛掷 10 次，同样的过程执行 5 轮，根据这 50 次投币的结果来计算 θ_A​ 和 θ_B​​ 的最大似然估计。

投掷硬币的过程，记录如下：

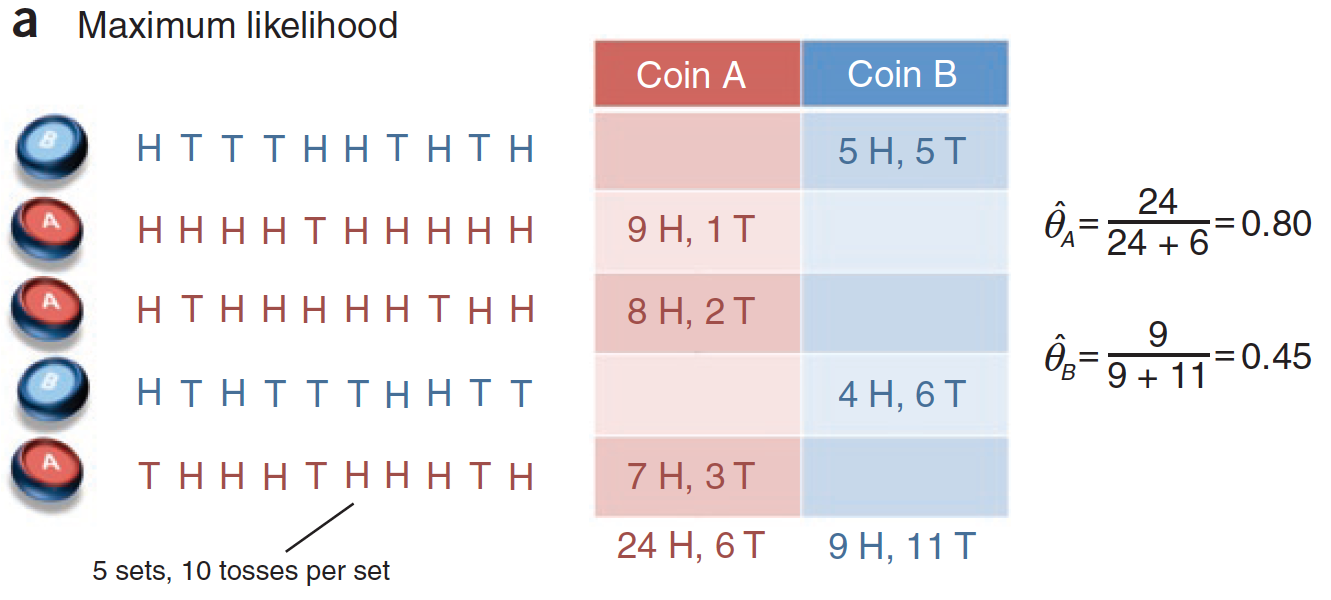
第1 到5 次分别投掷的硬币是 B，A，A，B，A。H 代表正面，T 代表负面。将上图转化为表格，如下：

次数	硬币	正面数	负面数
1	B	5	5
2	A	9	1
3	A	8	2
4	B	4	6
5	A	7	3

通过这个表格，可以直接计算 θ_A​ 和 θ_B​​，如下：

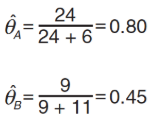
显然，如果知道每次投掷的硬币是A 还是B，那么计算θ_A​ 和 θ_B 是非常简单的。

但是，如果不知道每次投掷的硬币是A 还是B，该如何计算θ_A​ 和 θ_B 呢？

此时我们将上面表格中的硬币一列隐藏起来，这时硬币就是隐变量。所以我们只知道如下数据：

次数	正面数	负面数
1	5	5
2	9	1
3	8	2
4	4	6
5	7	3

这时想要计算 θ_A​ 和 θ_B，就要用最大似然估计的原理。

计算过程如下图：

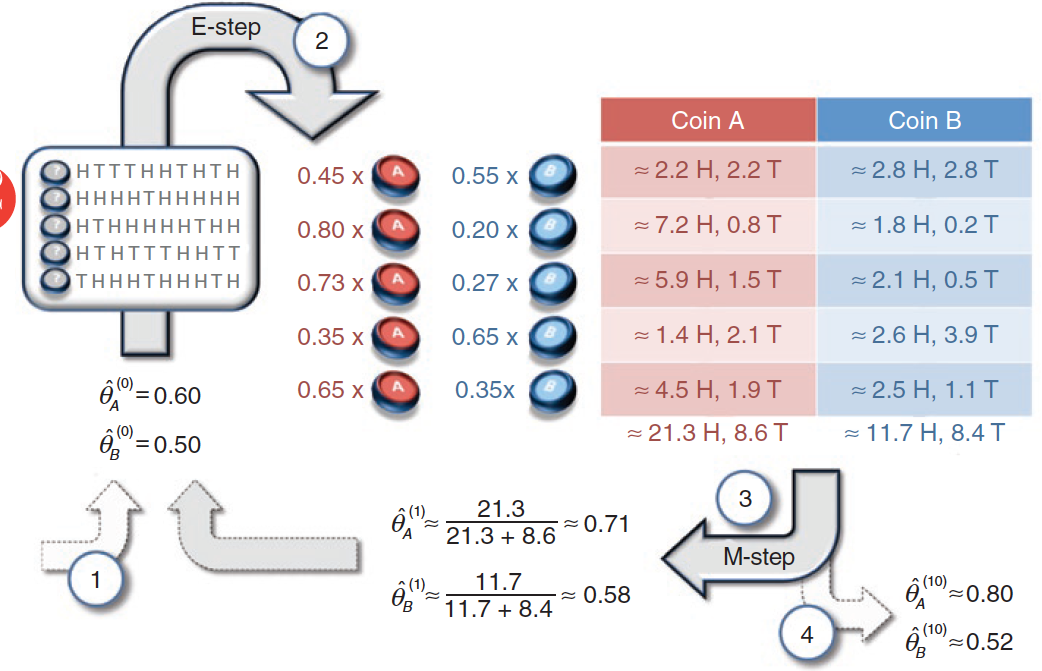
第一步

先为 θ_A​ 和 θ_B 设定一个初始值，比如 θ_A = 0.6，θ_B = 0.5。

第二步

我们知道每一轮投币的正 / 负面的次数：

• 第1轮：5 正 5 负，计算出现这种结果的概率：
  • 如果是A 硬币，那么P(H₅T₅|A) = 0.6^5 * 0.4^5
  • 如果是B 硬币，那么P(H₅T₅|B) = 0.5^5 * 0.5^5
  • 将 P(H₅T₅|A) 和 P(H₅T₅|B) 归一化处理，可得：
  • P(H₅T₅|A) = 0.45，P(H₅T₅|B) = 0.55
• 第2轮：9 正 1 负，计算出现这种结果的概率：
  • 如果是A 硬币，那么P(H₉T₁|A) = 0.6^9 * 0.4^1
  • 如果是B 硬币，那么P(H₉T₁|B) = 0.5^9 * 0.5^1
  • 将 P(H₉T₁|A) 和 P(H₉T₁|B) 归一化处理，可得：
  • P(H₉T₁|A) = 0.8，P(H₉T₁|B) = 0.2
• 第3轮：8 正 2 负，计算出现这种结果的概率：
  • 如果是A 硬币，那么P(H₈T₂|A) = 0.6^8 * 0.4^2
  • 如果是B 硬币，那么P(H₈T₂|B) = 0.5^8 * 0.5^2
  • 将 P(H₈T₂|A) 和 P(H₈T₂|B) 归一化处理，可得：
  • P(H₈T₂|A) = 0.73，P(H₈T₂|B) = 0.27
• 第4轮：4 正 6 负，计算出现这种结果的概率：
  • 如果是A 硬币，那么P(H₄T₆|A) = 0.6^4 * 0.4^6
  • 如果是B 硬币，那么P(H₄T₆|B) = 0.5^4 * 0.5^6
  • 将 P(H₄T₆|A) 和 P(H₄T₆|B) 归一化处理，可得：
  • P(H₄T₆|A) = 0.35，P(H₄T₆|B) = 0.65
• 第5轮：7 正 3 负，计算出现这种结果的概率：
  • 如果是A 硬币，那么P(H₇T₃|A) = 0.6^7 * 0.4^3
  • 如果是B 硬币，那么P(H₇T₃|B) = 0.5^7 * 0.5^3
  • 将 P(H₇T₃|A) 和 P(H₇T₃|B) 归一化处理，可得：
  • P(H₇T₃|A) = 0.65，P(H₇T₃|B) = 0.35

然后，根据每一轮的 P(H_mT_n|A) 和 P(H_mT_n|B)，可以计算出每一轮的正 / 负面次数。

m 为正面次数，n 为负面次数。

对于硬币A，结果如下：

轮数	P(HmTn|A)	m	n	正面数	负面数
1	0.45	5	5	0.45*5=2.2	0.45*5=2.2
2	0.8	9	1	0.8*9=7.2	0.8*1=0.8
3	0.73	8	2	0.73*8=5.9	0.73*2=1.5
4	0.35	4	6	0.35*4=1.4	0.35*6=2.1
5	0.65	7	3	0.65*7=4.5	0.65*3=1.9
总计	-	-	-	21.3	8.6

对于硬币B，结果如下：

轮数	P(HmTn|B)	m	n	正面数	负面数
1	0.55	5	5	0.55*5=2.8	0.55*5=2.8
2	0.2	9	1	0.2*9=1.8	0.2*1=0.2
3	0.27	8	2	0.27*8=2.1	0.27*2=0.5
4	0.65	4	6	0.65*4=2.6	0.65*6=3.9
5	0.35	7	3	0.35*7=2.5	0.35*3=1.1
总计	-	-	-	11.7	8.4

第三步

根据上面两个表格，可以得出（第1次迭代的结果） θ_A 和 θ_B：

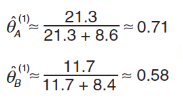
根据这个估计值，再次回到第一步去计算。

如此往复第一、二、三步，经过10次迭代之后，θ_A 和 θ_B 的估计值为：

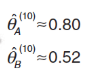
最终，θ_A 和 θ_B 将收敛到一个几乎不变的值，此时迭代结束。这样我们就求解出了θ_A 和 θ_B 的最大似然估计值。

我们将上述过程中，第一步称为初始化参数，第二步称为观察预期，第三步称为重新估计参数。

第一、二步为E 过程，第三步为M 过程，这就是EM 算法的过程。

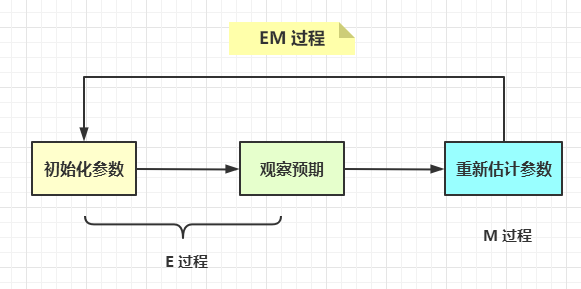
如果我们有一个待聚类的数据集，我们把潜在的类别当做隐变量，样本当做观察值，这样就可以把聚类问题转化成参数估计问题。这就是EM 聚类的原理。

6，硬聚类与软聚类

与 K 均值算法相比，K 均值算法是通过距离来区分样本之间的差别，且每个样本在计算的时候只能属于一个分类，我们称之为硬聚类算法。

而 EM 聚类在求解的过程中，实际上每个样本都有一定的概率和每个聚类相关，这叫做软聚类算法。

7，EM 聚类的缺点

EM 聚类算法存在两个比较明显的问题。

第一个问题是，EM 算法计算复杂，收敛较慢，不太适合大规模数据集和高维数据。

第二个问题是，EM 算法不一定能给出全局最优解：

• 当优化的目标函数是凸函数时，一定可以得到全局最优解。
• 当优化的目标函数不是凸函数时，可能会得到局部最优解，而非全局最优解。

8，GMM 高斯混合模型

上文中介绍过，常见的EM 算法有GMM 高斯混合模型和HMM 隐马尔科夫模型。这里主要介绍GMM 高斯混合模型的实现。

sklearn 库的mixture 模块中的GaussianMixture 类是GMM 算法的实现。

先来看下 GaussianMixture 类的原型：

GaussianMixture(
  n_components=1,
  covariance_type='full', 
  tol=0.001, 
  reg_covar=1e-06, 
  max_iter=100, 
  n_init=1, 
  init_params='kmeans', 
  weights_init=None, 
  means_init=None, 
  precisions_init=None, 
  random_state=None, 
  warm_start=False, 
  verbose=0, 
  verbose_interval=10)

这里介绍几个重要的参数：

• n_components：代表高斯混合模型的个数，也就是我们要聚类的个数，默认值为 1。
• covariance_type：代表协方差类型。一个高斯混合模型的分布是由均值向量和协方差矩阵决定的，所以协方差的类型也代表了不同的高斯混合模型的特征。协方差类型有 4 种取值：
  • full，代表完全协方差，也就是元素都不为 0；
  • tied，代表相同的完全协方差；
  • diag，代表对角协方差，也就是对角不为 0，其余为 0；
  • spherical，代表球面协方差，非对角为 0，对角完全相同，呈现球面的特性。
• max_iter：代表最大迭代次数，默认值为 100。

9，对鸢尾花数据集聚类

在《决策树算法-实战篇-鸢尾花及波士顿房价预测》中我们介绍过鸢尾花数据集。这里我们使用GMM 算法对该数据进行聚类。

首先加载数据集：

from sklearn.datasets import load_iris

iris = load_iris()   	# 加载数据集
features = iris.data	# 获取特征集
labels = iris.target    # 获取目标集

在聚类算法中，只需要特征数据 features，而不需要目标数据labels，但可以使用 labels 对聚类的结果做验证。

构造GMM聚类：

from sklearn.mixture import GaussianMixture

# 原数据中有 3 个分类，所以这里我们将 n_components 设置为 3
gmm = GaussianMixture(n_components=3, covariance_type='full')

对数据集进行聚类：

prediction_labels = gmm.fit_predict(features)

查看原始分类：

>>> print(labels)
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2]

查看聚类结果：

>>> print(prediction_labels)
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 2 1 2 1
 1 1 1 2 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 
 2 2]

对比原始分类和聚类结果，聚类结果中只有个别数据分类错误，我用红圈标了出来：

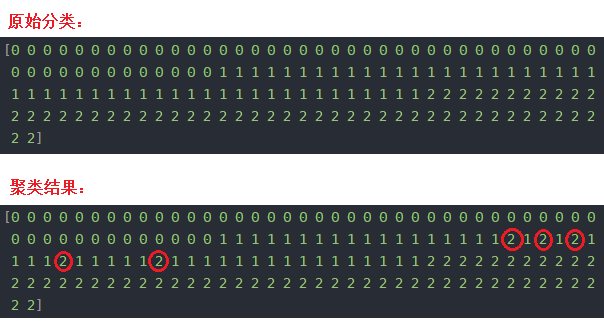
10，评估聚类结果

我们可以使用 Calinski-Harabaz 指标对聚类结果进行评估。

sklearn 库实现了该指标的计算，即 calinski_harabasz_score 方法，该方法会计算出一个分值，分数越高，代表聚类效果越好，也就是相同类中的差异性小，不同类之间的差异性大。

下面对鸢尾花数据集的聚类结果进行评估，传入特征数据和聚类结果：

>>> from sklearn.metrics import calinski_harabasz_score
>>> calinski_harabasz_score(features, prediction_labels)
481.78070899745234

我们也可以传入特征数据和原始结果：

>>> calinski_harabasz_score(features, labels)
487.33087637489984

可以看到，对于原始结果计算出的分值是487.33，对于预测结果计算出的分值是481.78，相差并不多，说明预测结果还是不错。

一般情况下，一个需要聚类的数据集并没有目标数据，所以只能对预测结果进行评分。我们需要人工对聚类的含义结果进行分析。

11，总结

本篇文章主要介绍了如下内容：

• EM 算法的过程及原理，介绍了一个投掷硬币的例子。
• 硬聚类与软聚类的区别。
• EM 聚类的缺点：
  • 计算复杂度较大。
  • 有可能得不到全局最优解。
• 使用GMM 算法对鸢尾花数据进行聚类。
• 使用 Calinski-Harabaz 指标对聚类结果进行评估。

（本节完。）

---

推荐阅读：

K 均值算法-如何让数据自动分组

Apriori 算法-如何进行关联规则挖掘

PageRank 算法-Google 如何给网页排名

数据变换-归一化与标准化

如何使用Python 进行数据可视化

---

欢迎关注作者公众号，获取更多技术干货。